1. 笛卡尔Nx, Ny, Nz方法

该方法特点如下：

• 用户自定义加密区域网格个数 （Nx, Ny, Nz）

• 线性插值

• 仅受源网格几何形态影响

以模型 Dxo=Dyo=149, Dzo=5为例，加密为: Nx=Ny=2, Nz=1，则结果如右图所示。

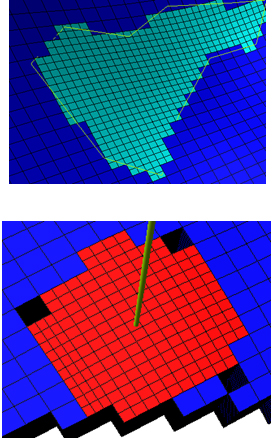
2. 笛卡尔Dx, Dy, Dz方法

• 用户自定义加密网格尺寸 （Dx, Dy, Dz）

• 等分源网格得到加密网格

• 仅受源网格几何尺寸影响

以模型 Dxo=Dyo=149, Dzo=5为例，进行加密: Dx=Dy=80, Dz=5，则通过计算Nx = Dxo / Dx与Ny = Dyo / Dy可得到加密结果，如右图所示。

3. 笛卡尔渐进式方法

笛卡尔渐进式方法提供三种方法，即整数法、对数法、小数法。软件在进行劈分时应用的核心理论为指数定律，其表达式为： 劈分网格数 = 基数 ^ 级数。其中，对数法可应用于笛卡尔网格与非结构化网格两种网格类型。

1）笛卡尔渐进式Nx, Ny, Nz方法

该方法操作如下：

• 用户自定义Nx, Ny, N

• 用户自定义不同的加密分级

• 用户自定义影响半径

首先讲述小数法，需要注意的是，若整数及对数均未被选中 ，则采用默认的小数法。以模型 Dxo=Dyo=149，Dzo=5为例，加密参数为: Nx=Ny=5， 级数=3，r=600，nx/ny: 2, 3, 5，那么将设定参数代入指数定律得：5=基数3，基数=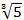 = 1.7，则劈分网格级数第1级为=5 ，第2级为 ，第3级为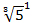 ，见下图左图。

如果应用整数法，将设定参数代入指数定律得：5=基数3，基数=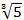≈ 2，则劈分网格级数第1级为23=8 ，第2级为22=4，第3级为21=2 ，见下图右图。

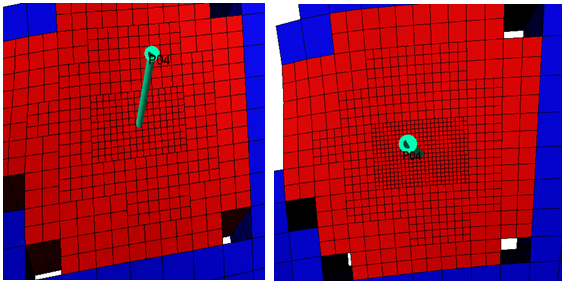
2）笛卡尔渐进式Dx, Dy, Dz方法

该方法操作如下：

• 用户自定义Dx, Dy, Dz

• 用户自定义加密分级

如果是小数法，以模型 Dxo=Dyo=149, Dzo=5, 级数=3为例，加密参数设定为 Dx=Dy=30，Dz=5，首先计算得到 Nx = Dxo/Dx = 5，Ny = Dyo/Dy = 5，然后应用指数定律得：5=基数3，基数=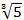= 1.7，则劈分网格级数第1级为=5 ，第2级为=3 ，第3级为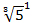=2 ，见下图左图。

如果是整数法，设置nx/ny: 2, 4, 8，则Nx = Dxo/Dx = 5，Ny = Dyo/Dy = 5，指数定律为 5=基数3，基数=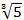≈ 2，则劈分网格级数第1级为23=8 ，第2级为22=4，第3级为21=2 ，见下图右图。

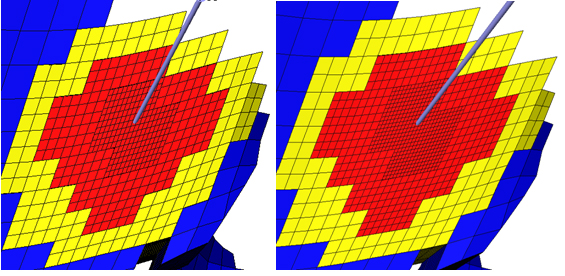
4. 对数法

1）对于笛卡尔网格：

xi=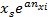 其中 nxi=1,2 ……. n

yi=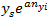 其中 nyi=1,2 ……. N

其中

a =下属劈分间距

nxi, nyi = 给定的劈分网格数

xi =每个下属劈分到源网格在x方向上的距离

xs =源网格对应于x轴的坐标

yi =每个下属劈分到源网格在y方向上的距离

ys = 源网格对应于y轴的坐标

2）对于非结构化网格

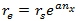
a = 下属劈分间距

nx = 给定的劈分网格数

rs = 影响半径

re = 每个下属劈分到源网格的距离

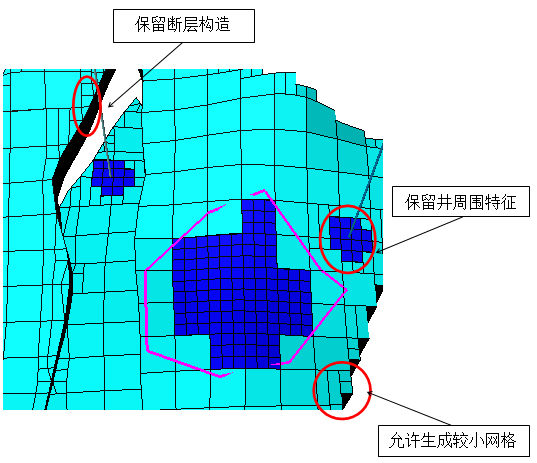
5. 粗化：

Petrel中的局部网格加密功能同样可以完成对网格的粗化需求。需要注意的是粗化时，被编辑网格的范围只能应用多边形（polygon）来筛选。粗化过程中用户可以自定义网格个数Nx，Ny，Nz，并可应用复合条件来控制生成的粗化网格的形态，控制条件如下：

• 保留断层构造

• 保留井周围特征 （可控制范围）

• 生成较小网格

• 粗化多边形边界外网格

• 延展源网格范围

下图为应用“粗化多边形边界外网格”控制条件生成粗化网格的例子，具体下属控制条件如图所示：