基于Petrel软件平台Function window窗口进行数据查看和分析时，经常会涉及到相关系数（Correlation coefficient；可用字母R或r表示）问题。例如在利用该窗口对两变量交会图（散点图）进行线性或非线性回归拟合的时候（即点击窗口顶部工具栏中的拟合按钮之后）。下面对其进行简要分析以便于合理使用。

在对该窗口中的两变量交会图（散点图）进行线性或非线性回归拟合时，在弹出窗口会显示线性或非线性回归方程以及对应的相关系数。由下图可见（假设两变量之间存在正弦相关关系），进行线性回归时（实为用最小二乘法拟合1次多项式；图中红线）弹出窗口显示的相关系数为-0.767931（负相关），而进行非线性回归时（软件此时默认用最小二乘法拟合2次多项式；图中绿线）则显示的是0.767931，弹出窗口将其称为Correlation index（为防止和中文中常见的相关指数概念混淆，这里暂不做翻译；比如中文中有时称R的平方为相关指数），其实际上应为相关系数的绝对值，所以仅看数值时无法知道是正相关还是负相关。进行非线性回归时，用户可以最高选择7次多项式进行拟合（Choose degree）。

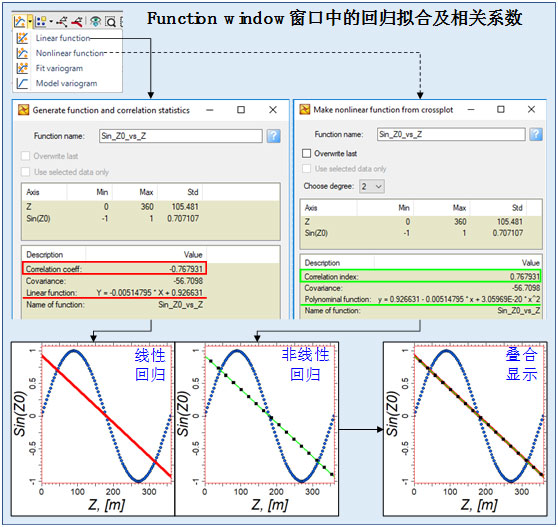
本实例线性回归时所得到的相关系数即为数学上最常见的两变量间的相关系数，其值等于两变量的协方差除以变量一的标准差和变量二的标准差，也即皮尔逊（Pearson）相关系数。那么这里非线性回归时的相关系数又该如何理解呢（先不管其实际为相关系数绝对值这一点）？变量还是那两个变量，为什么选择不同次的多项式进行拟合所得的相关系数不一样呢（例如本例中当选择用3次多项式进行拟合时，相关系数的绝对值则显示为0.995189）？ 其实不管是前述哪种回归拟合，都可以将显示的相关系数理解为回归方程（趋势线）的估计值（因变量）和对应的实际观测值之间的相关性（计算公式同前；另一个变量则为自变量）。

由前可见，本例中的线性回归所显示的相关系数与2次非线性回归所显示的相关系数几乎完全相等，这是因为2次多项式尚不足以能够较好地拟合如图所示的两变量间的复杂相关关系（正弦相关；这需要三次及以上多项式才能较好拟合）。

最后值得指出，Function window窗口中线性和非线性回归时所显示的相关系数与Microsoft Office Excel软件线性回归和高次多项式回归时所显示的R值（注意不是R的平方）是一致的；但Function window窗口中非线性回归时所显示的相关系数（绝对值）与利用Petrel Neural net功能进行神经网络训练时所出现的非线性相关系数（实为斯皮尔曼Spearman相关系数）是完全不同的两个概念。